METODA MONTE CARLO
27.11.2012
26.11.2012
APROKSYMACJA
Aproksymacja – proces określania rozwiązań przybliżonych na podstawie rozwiązań znanych, które są bliskie rozwiązaniom dokładnym w ściśle sprecyzowanym sensie. Zazwyczaj aproksymuje się byty (np. funkcje) skomplikowane bytami prostszymi.
Aproksymacja funkcji
Aproksymowanie funkcji może polegać na przybliżaniu jej za pomocą kombinacji liniowej tzw. funkcji bazowych. Od funkcji aproksymującej, przybliżającej zadaną funkcję nie wymaga się, aby przechodziła ona przez jakieś konkretne punkty, tak jak to ma miejsce w interpolacji. Z matematycznego punktu widzenia aproksymacja funkcji  w pewnej przestrzeni Hilberta
w pewnej przestrzeni Hilberta  jest zagadnieniem polegającym na odnalezieniu pewnej funkcji
jest zagadnieniem polegającym na odnalezieniu pewnej funkcji  gdzie
gdzie  jest podprzestrzenią
jest podprzestrzenią  tj.
tj.  takiej, by odległość (w sensie obowiązującej w
takiej, by odległość (w sensie obowiązującej w  normy) między
normy) między  a
a  była jak najmniejsza. Funkcja aproksymująca może wygładzać daną funkcję (gdy funkcja jest gładka, jest też różniczkowalna).
była jak najmniejsza. Funkcja aproksymująca może wygładzać daną funkcję (gdy funkcja jest gładka, jest też różniczkowalna).
Aproksymacja funkcji powoduje pojawienie się błędów, zwanych błędami aproksymacji. Dużą zaletą aproksymacji w stosunku do interpolacji jest to, że aby dobrze przybliżać, funkcja aproksymująca nie musi być wielomianem bardzo dużego stopnia (w ogóle nie musi być wielomianem). Przybliżenie w tym wypadku rozumiane jest jako minimalizacja pewnej funkcji błędu. Prawdopodobnie najpopularniejszą miarą tego błędu jest średni błąd kwadratowy, ale możliwe są również inne funkcje błędu, jak choćby błąd średni.
Istnieje wiele metod aproksymacyjnych. Jednymi z najbardziej popularnych są: aproksymacja średnio kwadratowa i aproksymacja jednostajna oraz aproksymacja liniowa, gdzie funkcją bazową jest funkcja liniowa.
Aproksymacja punktowa to rodzaj aproksymacji pozwalający przybliżyć zbiór punktów funkcją ciągłą. Aproksymacja ta, w odróżnieniu od większości innych metod aproksymacji, nie wymaga znajomości postaci analitycznej funkcji aproksymowanej.
PROCESY LOSOWE
- Procesem losowym nazywamy rodzinę zmiennych losowych

zależnych od parametru t i określonych na danej przestrzeni probabilistycznej (Ω,A,P).
Innymi słowy proces losowy to losowa funkcja parametru t, czyli taka funkcja, która  jest zmienną losowa.
jest zmienną losowa.
 jest zmienną losowa.
jest zmienną losowa.
Zmienną losową Xt, którą proces losowy jest w ustalonej chwili  nazywamy wartością tego procesu.
nazywamy wartością tego procesu.
 nazywamy wartością tego procesu.
nazywamy wartością tego procesu.
Zbiór wartości wszystkich zmiennych losowych  , nazywamy przestrzenią stanu procesu losowego lub przestrzenią stanu.
, nazywamy przestrzenią stanu procesu losowego lub przestrzenią stanu.
 , nazywamy przestrzenią stanu procesu losowego lub przestrzenią stanu.
, nazywamy przestrzenią stanu procesu losowego lub przestrzenią stanu.
Jeśli zbiór jest skończony lub przeliczalny, to mówimy o procesach losowych z czasem dyskretnym. W pierwszym wypadku mamy do czynienia z n-wymiarową zmienną losową, a w drugim z odpowiednim ciągiem zmiennych losowych.
Choć niektóre klasy procesów losowych z czasem dyskretnym (np. łańcuchy Markowa) zasługują na uwagę, to jednak w dalszym ciagu skoncentrujemy się na procesach losowych z czasem ciągłym czyli takich, dla których T jest nieprzeliczalne.
Dla głębszego zrozumienia natury procesu losowego spójrzmy nań jeszcze z innej strony. Jak pamiętamy zmienna losowa przyporządkowywała zdarzeniu losowemu punkt w przestrzeni Rn. W przypadku procesu losowego mamy do czynienia z sytuacją gdy do opisu wyniku doświadczenia niezbędna jest funkcja ciągła, zwana realizacją procesu losowego.
W dalszym ciągu zakładamy, że mamy do czynienia ze skończonymi funkcjami losowymi, a zbiór wszystkich takich funkcji (realizacji) będziemy nazywali przestrzenią realizacji procesu losowego. Prowadzi to do drugiej definicji:
W dalszym ciągu zakładamy, że mamy do czynienia ze skończonymi funkcjami losowymi, a zbiór wszystkich takich funkcji (realizacji) będziemy nazywali przestrzenią realizacji procesu losowego. Prowadzi to do drugiej definicji:
- Procesem losowym nazywamy mierzalną względem P transformację przestrzeni zdarzeń elementarnych Ω w przestrzeni realizacji, przy czym realizacją procesu losowego nazywamy każdą skończoną funkcją rzeczywistą zmiennej
 .
.
Definicja powyższa wynika ze spojrzenia na proces losowy jako na funkcję dwóch zmiennych  i
i  , ustalając t otrzymujemy zmienną losową , a ustalając ω otrzymujemy realizację .
, ustalając t otrzymujemy zmienną losową , a ustalając ω otrzymujemy realizację .
 i
i  , ustalając t otrzymujemy zmienną losową , a ustalając ω otrzymujemy realizację .
, ustalając t otrzymujemy zmienną losową , a ustalając ω otrzymujemy realizację .
Na ogół na przestrzeń realizacji procesu losowego narzuca się pewne ograniczenia np. żeby to była przestrzeń Banacha (niezerowa i zwyczajna).
Reasumując: graficznie można przedstawić te dwa punkty widzenia w następujacy sposób.
Pełne oznaczenie procesu losowego ma zatem postać
 , lub
, lub 
przy czym w obu wypadkach zakłada się, że jest określona przestrzeń probabilistyczna .
.
 , lub
, lub 
przy czym w obu wypadkach zakłada się, że jest określona przestrzeń probabilistyczna
 .
.
Ponieważ jednak zależność od ω jako naturalną zwykle się pomija, otrzymujemy:
 , lub
, lub  .
.
 , lub
, lub  .
.
Ponadto, jeśli zbiór T jest zdefiniowany na początku rozważań to pomija się także zapis  i w rezultacie otrzymujemy :
i w rezultacie otrzymujemy :
Xt, lub X(t).
 i w rezultacie otrzymujemy :
i w rezultacie otrzymujemy :Xt, lub X(t).
Oznaczenie X(t) może zatem dotyczyć całego procesu losowego, jego jednej realizacji (dla ustalonego ω) lub jego jednej wartości, czyli zmiennej losowej (dla ustalonego t). Z kontekstu jednoznacznie wynika, o co w danym zapisie chodzi.
Przejdźmy do zapisu procesu losowego X(t). Będziemy rozpatrywać wyłącznie procesy losowe rzeczywiste (proces losowy zespolony ma postać: X(t) = X1(t) + iX2(t), gdzie X1(t) i X2(t) są procesami losowymi rzeczywistymi).
Ponieważ  proces losowy Xt jest zmienną, więc jego pełny opis w chwili t stanowi pełny rozkład prawdopodobieństwa tej zmiennej losowej. Rozkład taki nazywamy jednowymiarowym rozkładem prawdopodobieństwa procesu losowego. Jest on scharakteryzowany przez jednowymiarową dystrybuantę procesu losowego, w postaci :
proces losowy Xt jest zmienną, więc jego pełny opis w chwili t stanowi pełny rozkład prawdopodobieństwa tej zmiennej losowej. Rozkład taki nazywamy jednowymiarowym rozkładem prawdopodobieństwa procesu losowego. Jest on scharakteryzowany przez jednowymiarową dystrybuantę procesu losowego, w postaci :
F(x,t) = P[X(t) < x]
 proces losowy Xt jest zmienną, więc jego pełny opis w chwili t stanowi pełny rozkład prawdopodobieństwa tej zmiennej losowej. Rozkład taki nazywamy jednowymiarowym rozkładem prawdopodobieństwa procesu losowego. Jest on scharakteryzowany przez jednowymiarową dystrybuantę procesu losowego, w postaci :
proces losowy Xt jest zmienną, więc jego pełny opis w chwili t stanowi pełny rozkład prawdopodobieństwa tej zmiennej losowej. Rozkład taki nazywamy jednowymiarowym rozkładem prawdopodobieństwa procesu losowego. Jest on scharakteryzowany przez jednowymiarową dystrybuantę procesu losowego, w postaci :F(x,t) = P[X(t) < x]
Oczywiście rozkład jednowymiarowy procesu losowego nie charakteryzuje wzajemnej zależności między wartościami procesu (zmiennymi losowymi) w różnych chwilach. Jest on zatem ogólny tylko wtedy gdy dla dowolnych układów  wartości procesu losowego,są ciągami zmiennych losowych niezależnych, co na ogół nie zachodzi. W ogólności musimy zatem rozpatrywać łączny rozkład wartości procesu w różnych chwilach.
wartości procesu losowego,są ciągami zmiennych losowych niezależnych, co na ogół nie zachodzi. W ogólności musimy zatem rozpatrywać łączny rozkład wartości procesu w różnych chwilach.
 wartości procesu losowego,są ciągami zmiennych losowych niezależnych, co na ogół nie zachodzi. W ogólności musimy zatem rozpatrywać łączny rozkład wartości procesu w różnych chwilach.
wartości procesu losowego,są ciągami zmiennych losowych niezależnych, co na ogół nie zachodzi. W ogólności musimy zatem rozpatrywać łączny rozkład wartości procesu w różnych chwilach.25.11.2012
11.11.2012
KORELACJA
Zależność statystyczna zmiennych losowych– związek pomiędzy dwiema zmiennymi losowymi X i Y.
Intuicyjnie, zależność dwóch zmiennych oznacza, że znając wartość jednej z nich, dałoby się przynajmniej w niektórych sytuacjach dokładniej przewidzieć wartość drugiej zmiennej, niż bez tej informacji.
Współczynnik korelacji liniowej
Jednym z najważniejszych mierników wykorzystywanych w analizie korelacji, określania w jakim stopniu zmienne są współzależne lub inaczej też określa poziom zależności liniowej między zmiennymi losowymi, jest współczynnik korelacji liniowej Pearsona.
Jego formuła obliczeniowa jest następująca
rxy = cov(xy) / S(x) * S(y)
współczynnik jest symetryczny czyli
rxy = ryx
Przyjęto oceniać, na podstawie wyniku i znaku, siłę i kierunek współzależności w następujący sposób:
/0,0-0,2/ - współzależność bardzo słaba
/0,2-0,4/ - współzależność słaba
/0,4-0,6/ - współzależność umiarkowana
/0,6-0,8/ - współzależność silna
/0,8-1,0/ - współzależność bardzo silna
Zależność a współczynnik korelacji
Często błędnie zakłada się, że zależność statystyczna jest równoważna niezerowemu współczynnikowi korelacji. Nie jest to prawda. Na przykład zmienne X i Y mogą być związane zależnością:METODY ITERACYJNE
Metoda Gaussa - Seidela jest metodą iteracyjną i pozwala nam obliczyć układ n równań z n niewiadomymi Ax = b. Wektor x0 będący początkowym przybliżeniem rozwiązania układu będzie dany (zwykle przyjmuje się go jako wektor złożony z samych zer). By zastosować tą metodę należy najpierw tak zamienić kolejność równań układu, aby na głównej przekątnej były elementy różne od zera.
Na początku macierz współczynników A rozłożymy na sumę trzech macierzy A = L + D + U, gdzie L jest macierzą w której znajdują się elementy których numer wiersza jest większy od numeru kolumny, D to macierz diagonalna z elementami tylko na głównej przekątnej, a U to macierz, w której znajdują się elementy których numery wiersza są mniejsze od numerów kolumny. Można to zapisać następująco:
Rozpatrzmy układ
 równań liniowych z
równań liniowych z  niewiadomymi:
niewiadomymi:gdzie
 jest nieosobliwą macierzą diagonalną, a
jest nieosobliwą macierzą diagonalną, a  i
i  są odpowiednio macierzą dolnotrójątnąi górnotrójkątną macierzy
są odpowiednio macierzą dolnotrójątnąi górnotrójkątną macierzy  (tzn.
(tzn.  oraz
oraz  mają zera na głównej przekątnej oraz
mają zera na głównej przekątnej oraz  ), natomiast indeks
), natomiast indeks 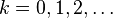 oznacza numer porządkowy iteracji.
oznacza numer porządkowy iteracji.Po rozpisaniu na składowe wzór ten przyjmuje postać używaną w implementacjach numerycznych:
 Metoda Gaussa-Seidla jest metodą relaksacyjną, w której poszukiwanie
rozwiązania rozpoczyna się od dowolnie wybranego rozwiązania próbnego ,
po czym w kolejnych krokach, zwanych iteracjami, za pomocą prostego
algorytmu zmienia się kolejno jego składowe, tak by coraz lepiej
odpowiadały rzeczywistemu rozwiązaniu.
Metoda Gaussa-Seidla jest metodą relaksacyjną, w której poszukiwanie
rozwiązania rozpoczyna się od dowolnie wybranego rozwiązania próbnego ,
po czym w kolejnych krokach, zwanych iteracjami, za pomocą prostego
algorytmu zmienia się kolejno jego składowe, tak by coraz lepiej
odpowiadały rzeczywistemu rozwiązaniu.
Metoda Gaussa-Seidla bazuje na metodzie Jacobiego, w której krok iteracyjny zmieniono w ten sposób, by każda modyfikacja rozwiązania próbnego korzystała ze wszystkich aktualnie dostępnych przybliżonych składowych rozwiązania. Pozwala to zaoszczędzić połowę pamięci operacyjnej i w większości zastosowań praktycznych zmniejsza ok. dwukrotnie liczbę obliczeń niezbędnych do osiągnięcia zadanej dokładności rozwiązania.
Subskrybuj:
Posty (Atom)








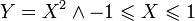
 ,
, – zadany wektor (
– zadany wektor ( – poszukiwane rozwiązanie (wektor o
– poszukiwane rozwiązanie (wektor o 
 Metoda Gaussa-Seidla jest metodą relaksacyjną, w której poszukiwanie
rozwiązania rozpoczyna się od dowolnie wybranego rozwiązania próbnego ,
po czym w kolejnych krokach, zwanych iteracjami, za pomocą prostego
algorytmu zmienia się kolejno jego składowe, tak by coraz lepiej
odpowiadały rzeczywistemu rozwiązaniu.
Metoda Gaussa-Seidla jest metodą relaksacyjną, w której poszukiwanie
rozwiązania rozpoczyna się od dowolnie wybranego rozwiązania próbnego ,
po czym w kolejnych krokach, zwanych iteracjami, za pomocą prostego
algorytmu zmienia się kolejno jego składowe, tak by coraz lepiej
odpowiadały rzeczywistemu rozwiązaniu.