METODY ITERACYJNE
Metoda Gaussa - Seidela jest metodą iteracyjną i pozwala nam obliczyć układ n równań z n niewiadomymi Ax = b. Wektor x0 będący początkowym przybliżeniem rozwiązania układu będzie dany (zwykle przyjmuje się go jako wektor złożony z samych zer). By zastosować tą metodę należy najpierw tak zamienić kolejność równań układu, aby na głównej przekątnej były elementy różne od zera.
Na początku macierz współczynników A rozłożymy na sumę trzech macierzy A = L + D + U, gdzie L jest macierzą w której znajdują się elementy których numer wiersza jest większy od numeru kolumny, D to macierz diagonalna z elementami tylko na głównej przekątnej, a U to macierz, w której znajdują się elementy których numery wiersza są mniejsze od numerów kolumny. Można to zapisać następująco:
Rozpatrzmy układ
 równań liniowych z
równań liniowych z  niewiadomymi:
niewiadomymi:gdzie
 jest nieosobliwą macierzą diagonalną, a
jest nieosobliwą macierzą diagonalną, a 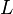 i
i  są odpowiednio macierzą dolnotrójątnąi górnotrójkątną macierzy
są odpowiednio macierzą dolnotrójątnąi górnotrójkątną macierzy  (tzn.
(tzn. 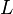 oraz
oraz  mają zera na głównej przekątnej oraz
mają zera na głównej przekątnej oraz  ), natomiast indeks
), natomiast indeks 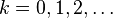 oznacza numer porządkowy iteracji.
oznacza numer porządkowy iteracji.Po rozpisaniu na składowe wzór ten przyjmuje postać używaną w implementacjach numerycznych:
 Metoda Gaussa-Seidla jest metodą relaksacyjną, w której poszukiwanie
rozwiązania rozpoczyna się od dowolnie wybranego rozwiązania próbnego ,
po czym w kolejnych krokach, zwanych iteracjami, za pomocą prostego
algorytmu zmienia się kolejno jego składowe, tak by coraz lepiej
odpowiadały rzeczywistemu rozwiązaniu.
Metoda Gaussa-Seidla jest metodą relaksacyjną, w której poszukiwanie
rozwiązania rozpoczyna się od dowolnie wybranego rozwiązania próbnego ,
po czym w kolejnych krokach, zwanych iteracjami, za pomocą prostego
algorytmu zmienia się kolejno jego składowe, tak by coraz lepiej
odpowiadały rzeczywistemu rozwiązaniu.
Metoda Gaussa-Seidla bazuje na metodzie Jacobiego, w której krok iteracyjny zmieniono w ten sposób, by każda modyfikacja rozwiązania próbnego korzystała ze wszystkich aktualnie dostępnych przybliżonych składowych rozwiązania. Pozwala to zaoszczędzić połowę pamięci operacyjnej i w większości zastosowań praktycznych zmniejsza ok. dwukrotnie liczbę obliczeń niezbędnych do osiągnięcia zadanej dokładności rozwiązania.
 ,
, – zadany wektor (
– zadany wektor ( – poszukiwane rozwiązanie (wektor o
– poszukiwane rozwiązanie (wektor o 
 Metoda Gaussa-Seidla jest metodą relaksacyjną, w której poszukiwanie
rozwiązania rozpoczyna się od dowolnie wybranego rozwiązania próbnego ,
po czym w kolejnych krokach, zwanych iteracjami, za pomocą prostego
algorytmu zmienia się kolejno jego składowe, tak by coraz lepiej
odpowiadały rzeczywistemu rozwiązaniu.
Metoda Gaussa-Seidla jest metodą relaksacyjną, w której poszukiwanie
rozwiązania rozpoczyna się od dowolnie wybranego rozwiązania próbnego ,
po czym w kolejnych krokach, zwanych iteracjami, za pomocą prostego
algorytmu zmienia się kolejno jego składowe, tak by coraz lepiej
odpowiadały rzeczywistemu rozwiązaniu.
Brak komentarzy:
Prześlij komentarz